
FastPlasmaSim
Acceleration of Free-boundary Grad-Shafranov codes using advanced numerical methods

Abstract
Controlled fusion reactions hold great promise for sustainable energy production. By mimicking the processes that power the sun, fusion could provide a nearly limitless, clean, and safe energy source with minimal greenhouse gas emissions and significantly less radioactive waste compared to traditional nuclear fission. However, despite its potential, fusion energy is not yet commercially viable, and significant research is still needed.
To support the complex computational needs of fusion development, the European Consortium for the Development of Fusion Energy (EUROfusion) has selected EPFL as one of their Advanced Computing Hubs. Led by the Swiss Plasma Center (SPC), this hub integrates expertise from EPFL’s Institute of Mathematics, SCITAS (a high-performance scientific computing platform), the Swiss Data Science Center (SDSC), and the Laboratory for Experimental Museology (eM+). This collaborative effort will enhance the computational capacity required for cutting-edge fusion simulations, driving forward the quest for sustainable and secure energy solutions.
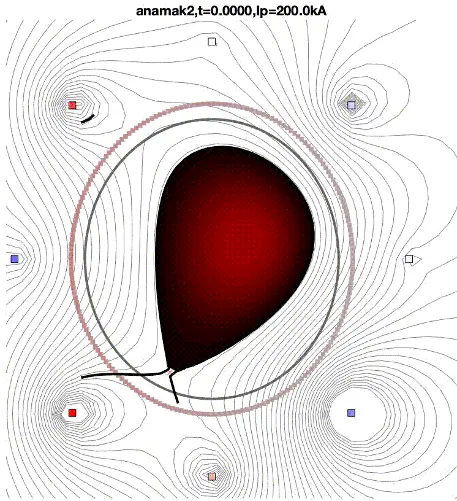
Within this context, the SDSC and the SPC are teaming up for a first collaboration to implement and accelerate free-boundary Grad-Shafranov codes (FGS/FGE/LIU) using advanced numerical methods, including machine learning. These codes, integrated within the MEQ code collection, solves the Grad-Shafranov equation (axisymmetric ideal Magnetohydrodynamics force balance, see Figure 1) and are a key component of workflows for tokamak modeling, having applications in integrated modeling, discharge pre-simulation and preparation, magnetic control design and validation.
People
Collaborators


Alessandro holds an M.Sc. in Applied Mathematics from EPFL with a minor in Data Science. After his studies, he joined the SDSC as Data Scientist in April 2022, where he closely works with the academic community to enlarge and support the use of data science. Over the years he worked on a variety of topics, from extreme events modeling to time series representation. His main interest lies in the application of machine learning to the energy sector.


Guillaume Obozinski graduated with a PhD in Statistics from UC Berkeley in 2009. He did his postdoc and held until 2012 a researcher position in the Willow and Sierra teams at INRIA and Ecole Normale Supérieure in Paris. He was then Research Faculty at Ecole des Ponts ParisTech until 2018. Guillaume has broad interests in statistics and machine learning and worked over time on sparse modeling, optimization for large scale learning, graphical models, relational learning and semantic embeddings, with applications in various domains from computational biology to computer vision.
PI | Partners:
description
Motivation
Acceleration of these Free-boundary Grad-Shafranov codes is of particular importance for so-called tokamak ‘flight simulators’ that are being developed to test a tokamak discharge before it is run. Such simulators should be able to simulate the entire discharge from the coil magnetization until termination and is expected to be a key component of future tokamak operations including ITER and DEMO. Ideally, these flight simulators should operate at speeds exceeding real-time to allow testing of the plasma control system in a realistic setting. Furthermore, faster-than-real-time Grad-Shafranov solvers enable routine use of optimization methods to improve tokamak operations, e.g., by optimizing poloidal field coil current evolution to maximize discharge duration or minimize structural forces.
Proposed Approach / Solution
Formulating the solution to the Grad-Shafranov equation (FGS/FGE) involves solving a set of nonlinear equations in a high-dimensional space. The current method, a Newton schema called Jacobian-Free Newton Krylov (JFNK), addresses the challenge of Jacobian inversion costs by employing a Krylov iterative method (GMRES) and substituting Jacobian-vector products with finite differences. However, the effectiveness of this approach relies on finding good preconditioners to diminish the search dimension in the Krylov space.
We proposed an improvement of the vanilla Broyden method that leverages on the structure of the Grad-Shafranov equations, particularly the spatial localization of the plasma, resulting in sparse Jacobian. While the vanilla Broyden method constructs and maintains an approximation of the inverse Jacobian, thereby avoiding inversion costs and the necessity for effective preconditioners, its complexity remains comparable to the JFNK method. However, we achieved a reduction in computational, by maintaining a low-rank approximation of a structured decomposition of the inverse Jacobian to speed up matrix-vector products.
Building on these results, the method is currently being adapted to the LIU code, which reconstructs plasma boundary shapes from measured datapoints, by solving a constrained minimization problem where the FGS code acts as a physical constraint. This aims at improving the current solver, which is based on a Sequential Quadratic Programming (SQP) approach.
Impact
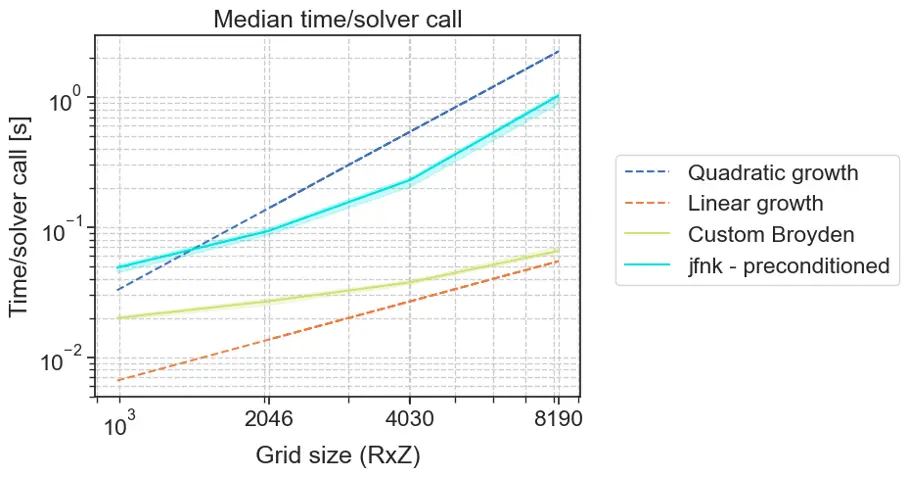
The code employing the Broyden method, which has been released in the MEQ suite, offers more than two-fold speed up in comparison to the JFNK solver (Figure 2), while keeping the convergence properties of the latter. The complexity is further reduced to linear due to the low rank approximation, which is a step towards real-time simulations and accelerates other code relying on FGS/FGE as subroutine.
Presentation
Gallery
Annexe
Additional resources
Bibliography
- Carpanese, F. (2021). Development of free-boundary equilibrium and transport solvers for simulation and real-time interpretation of tokamak experiments. 238. doi:10.5075/epfl-thesis-7914
- Knoll, D. A., & Keyes, D. E. (2004). Jacobian-free Newton–Krylov methods: a survey of approaches and applications. Journal of Computational Physics, 193(2), 357-397.
- Fang, H. R., & Saad, Y. (2009). Two classes of multisecant methods for nonlinear acceleration. Numerical linear algebra with applications, 16(3), 197-221.
Publications
Related Pages
More projects
OneDoc 'Ask Doki'
SFOE Energy Dashboard
Enhancing resource efficiency
News
Latest news


Data Science & AI Briefing Series for Executives
Data Science & AI Briefing Series for Executives


PAIRED-HYDRO | Increasing the Lifespan of Hydropower Turbines with Machine Learning
PAIRED-HYDRO | Increasing the Lifespan of Hydropower Turbines with Machine Learning


First National Calls: 50 selected projects to start in 2025
First National Calls: 50 selected projects to start in 2025
Contact us
Let’s talk Data Science
Do you need our services or expertise?
Contact us for your next Data Science project!




