This blog post is devoted to our ICLR2024 paper: “Efficient and Scalable Graph Generation through Iterative Local Expansion”.
Summary
Have you ever considered the complexity of generating large-scale, intricate graphs akin to those that represent the vast relational structures of our world? Our research introduces a pioneering approach to graph generation that tackles the scalability and complexity of creating such expansive, real-world graphs. Traditional methods often struggle with computational efficiency and the fidelity of generated samples as graph size increases. Drawing inspiration from natural growth patterns, we model graph generation as a progressive expansion process, starting from a single node and iteratively growing it to a complete graph. We present a new neural network architecture, Local PPGN, tailored to our approach to graph generation. It is efficient on sparse graphs and offers enhanced expressiveness. Our experiments show that our model surpasses existing scalability methods and generates structurally accurate graphs that mirror the training data, even for graph sizes not encountered during training.
Graph generation
Graphs are mathematical structures used to model a set of objects represented as nodes, and the relationships between them, represented as edges. They offer a practical means of abstracting discrete data across various fields, from social networks, where nodes and edges represent individuals and their friendships, to chemistry, where they correspond to atoms and bonds, and transportation, where they signify cities and roads.
Unsurprisingly, generating new graphs with specific properties holds immense potential, such as searching for new drug candidates. However, graph generation presents unique challenges. Unlike well-studied areas like image or text generation, graphs are inherently irregular and complex, making their creation a less explored area of research.
This blog post delves into our innovative approach to graph generation [1], focusing on unattributed graphs where nodes and edges carry no additional information.
Existing challenges
Contemporary graph generation strategies can be broadly categorized into autoregressive or one-shot methods. Autoregressive techniques build graphs incrementally, predicting edges for each new node. In contrast, one-shot methods generate the entire graph structure at once using generative frameworks such as variational autoencoders, generative adversarial networks, normalizing flows, or diffusion models instantiated with permutation-invariant graph neural networks. Despite the success of these methods in generating graphs comprising several hundred nodes, a persistent challenge lies in effectively scaling the generation process to produce large graphs while maintaining their real-world complexities. The computational complexity of these methods is at least quadratic for the number of nodes since a prediction must be made for each possible pair of nodes to determine if an edge connects them. This approach is inefficient for sparse graphs typical of real-world data. Sample fidelity is also an issue, as autoregressive methods struggle with node-permutation-invariant training due to the factorial increase in node orderings, and one-shot methods often fail to capture both global and local graph structure simultaneously. Additionally, the neural architectures used either lack expressiveness or are computationally expensive.
Paradigm shift
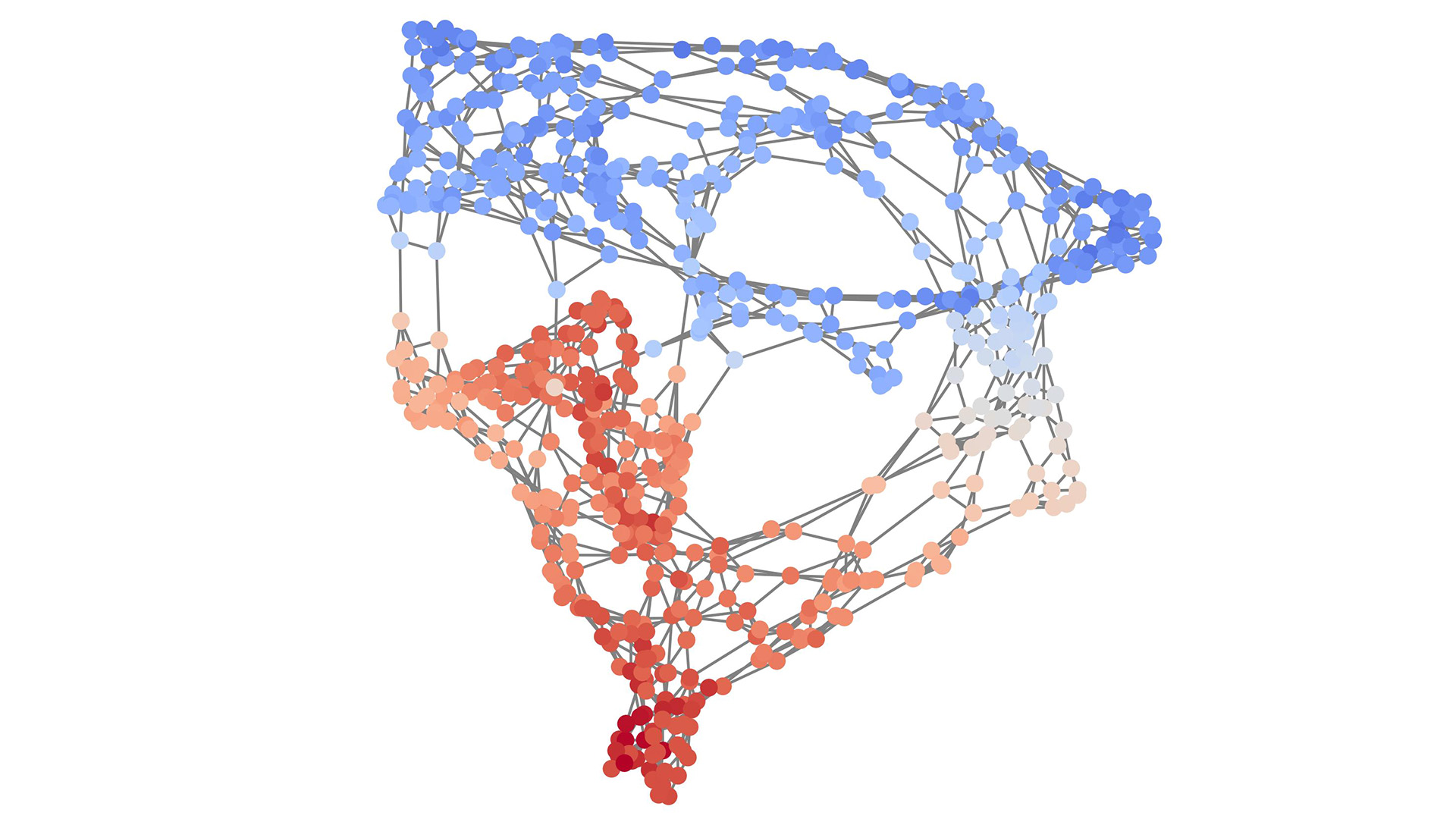
To address these challenges, we propose a novel paradigm for graph generation. Rather than directly attempting to generate the target graph, our approach models a progressive graph growth process inspired by the organic growth patterns observed in natural systems. Consider the growth of a tree – the robust trunk and primary branches establish the global structure before finer branches and leaves emerge. In urban planning, the layout of major transport routes, residential areas, and commercial centers is established first, setting the framework of the city's overarching structure. Planning then progresses to the detail of individual neighborhoods, local roadways, parks, and buildings with unique architectural features. Given that we usually only have access to samples of graphs rather than their generative processes, we propose to reverse-engineer this process through graph coarsening. By learning to invert the graph coarsening process, as illustrated in Figure 1, we can progressively expand a single node into a full-sized graph - the essence of our graph generation method.

Graph coarsening
Graph coarsening is a technique that reduces the size of a graph by merging nodes while striving to preserve its overarching structure. This process is analogous to reducing the resolution of an image while maintaining its recognizability. Our work adopts a multi-level graph coarsening technique where each level identifies and contracts interconnected subgraphs into single nodes [2]. The selection of subgraphs is optimized to maintain the essential structure of the graph even as it is simplified. Understanding this process is crucial to our approach, as we aim to invert this coarsening process to generate new graphs.
Inverting graph coarsening
The essence of our novel approach lies in learning to invert each step in a coarsening process, effectively enabling us to sample new graphs by iteratively expanding a single node into a full-sized graph. To elucidate this, let us delve into our proposed idea to invert a coarsening step. Take a graph \(G = (V, E)\), where \(V\) is the set of nodes and \(E\) is the set of edges. Now consider a coarsened version of \(G\), denoted as \(\bar{G} = (\bar{V}, \bar{E})\). In this coarsened graph, each node \(v^{(p)} \in \bar{V}\) corresponds to a cluster of connected nodes \(V^{(p)} \subseteq V\) from the original graph \(G\). The edge set \(\bar{E}\) connects nodes \(v^{(p)}\) and \(v^{(q)}\) if there is at least one edge connecting any node in \(V^{(p)}\) to any node in \(V^{(q)}\) in the original graph \(G\). As illustrated in Figure 2, reversing the coarsening involves a two-step process. First, we expand the coarsened graph by replacing each node \(v^{(p)}\) with a fully connected cluster of size \(|V^{(p)}|\) and by adding edges to connect nodes in adjacent clusters. This expansion results in a graph \(\tilde{G}\), which has the same number of nodes as the original graph \(G\) and contains all of its edges, plus possibly some additional ones. In the second step, we prune the excess edges from \(\tilde{G}\) to recover the original graph \(G\).

Method
To generate graphs, we must learn how many nodes to expand into and which edges to remove. We frame this as a feature learning problem - node features corresponding to expansion size and binary edge features corresponding to edge removal. We propose to learn a distribution over these features using denoising diffusion [3], a recently proposed generative method that has shown state-of-the-art performance in image generation and other domains. Sampling from these distributions allows us to reverse the coarsening process probabilistically. Since denoising diffusion sampling is iterative, our approach effectively becomes a nesting of two iterative processes: the denoising diffusion sampling and the iterative expansion.
Training
For model training, we construct coarsening sequences of graphs, as illustrated in Figure 1, by applying a randomized version of the graph coarsening method described in section Graph coarsening to a dataset of graphs. In each training step, we select pairs of consecutive graphs from the constructed sequences and derive the node and edge features needed to expand and refine the smaller graph into the larger one. These features are then perturbed with noise using the denoising diffusion framework, and the model is trained to predict the original, noise-free features. Our paper demonstrates that this training process optimizes a lower bound on the data log-likelihood.
Complexity
Our approach to graph generation stands out for its efficiency and scalability. By adopting a hierarchical strategy, we circumvent the need to predict connections between every node pair, allowing us to generate sparse graphs with subquadratic complexity in the number of nodes. Specifically, in each expansion step of a generation process, we increase the graph's size by a constant factor, enabling us to construct a graph with \(n\) nodes in \(O(\log n)\) steps. When each step is executed efficiently—for instance, linearly proportional to the number of edges, we can generate a graph with \(n\) nodes and \(m\) edges in \(O(m \log n)\) time. This technique substantially improves the quadratic complexity of many current methods, especially for sparse graphs where \(m\) is significantly smaller than \(n^2\).
The critical element in each step of the iterative expansion is the sampling of node and edge features required for refining the expanded graph. Performing this efficiently requires an efficient parameterization of the denoising diffusion model. Message-passing neural networks are a natural choice for this purpose, as they exhibit linear complexity in the number of edges. However, they are limited in expressiveness, only as discriminative as the Weisfeiler-Lehman graph isomorphism test, meaning they cannot differentiate between certain non-isomorphic graphs [4]. Provably Powerful Graph Neural Networks (PPGNs) [5] offer a more expressive alternative but at the cost of cubic complexity in the number of nodes. To balance this trade-off, we propose a novel architecture, termed Local PPGN, which restricts the global aggregation of PPGNs to a local one. This new architecture is locally expressive and maintains efficiency on sparse graphs.
Experiments
We validated our method empirically by comparing it against existing baselines on standard benchmark datasets. These datasets include synthetic planar, tree, stochastic block model graphs, and real-world protein and point cloud graphs. Our method achieves a new record Validity-Uniqueness-Novelty score for synthetic planar and tree graphs. This metric quantifies the proportion of generated graphs that are both valid and non-isomorphic to any other generated graph or any graph in the training set. Additionally, our method generates graphs that most closely match the test set's structural statistics for protein and point cloud datasets. Figures 3 and 4 compare the test set graphs and those generated by our method for planar and protein datasets, respectively.


We posit that the growth process our model learns exhibits greater robustness to variations in graph sizes compared to existing methods. To verify this, we generated graphs with an unseen number of nodes during training and verified if they retained the training data's defining characteristics. Our method is the only one capable of preserving these characteristics across the considered datasets, demonstrating its ability to generalize beyond the training distribution. Figure 5 shows generated planar and tree graphs from a model trained on significantly smaller graphs.

Lastly, we assess the scalability of our method by generating planar graphs of different sizes. The results demonstrate that our approach scales almost linearly with the number of nodes, a performance comparable to other scalable methods that fall short in sample fidelity. Significantly, our method outperforms existing methods that exhibit quadratic or higher scaling behavior while maintaining high sample fidelity.
Conclusion
Our research presents a novel and efficient approach to graph generation that can scale to large graphs without compromising structural fidelity. The Local PPGN architecture is particularly well-suited for this task, balancing efficiency and expressiveness. Our findings have the potential to impact various domains where graph generation plays a crucial role, such as in biology, medicine, or transportation planning, opening new avenues for exploration and innovation.
Have we sparked your interest? Dive into the details of our work by reading the entire paper and by exploring our implementation on GitHub.
For more information about the author, head over to andreasbergmeister.github.io.
Co-authors
- Karolis Martinkus, Prescient Design, Genentech, Roche
- Nathanaël Perraudin, Swiss Data Science Center, ETH Zurich
- Roger Wattenhofer, DISCO, ETH Zürich
References
- Andreas Bergmeister, Karolis Martinkus, Nathanaël Perraudin, Roger Wattenhofer. (2023) "Efficient and Scalable Graph Generation through Iterative Local Expansion". https://doi.org/10.48550/arXiv.2312.11529
- Andreas Loukas. (2018) "Graph reduction with spectral and cut guarantees". https://doi.org/10.48550/arXiv.1808.10650
- Yang Song, Jascha Sohl-Dickstein, Diederik P. Kingma, Abhishek Kumar, Stefano Ermon, Ben Poole. (2020) "Score-Based Generative Modeling through Stochastic Differential Equations". https://doi.org/10.48550/arXiv.2011.13456
- Keyulu Xu, Weihua Hu, Jure Leskovec, Stefanie Jegelka. (2018) "How Powerful are Graph Neural Networks?". https://doi.org/10.48550/arXiv.1810.00826
- Haggai Maron, Heli Ben-Hamu, Hadar Serviansky, Yaron Lipman. (2019) "Provably Powerful Graph Networks". https://doi.org/10.48550/arXiv.1905.11136